Most of the diagrams are direct from web sites so I apologise if there are any copyright issues "“ I only want to pass on information for the education of others and am not making any monetary gain from this and do not claim the information as my own and any mistakes are purely my own. If there are any problems please let me know through this forum and the particular information will be either corrected or removed. Thank You.
So onwards
As I stated in an earlier post "“ the direction the sun is viewed is a great circle viewed from the surface of an oblate spheroid (the Earth).To make things clearer I will first introduce and explain a few terms for those that may not be familiar with them "“ and maybe a refresher for others.
CIRCLES
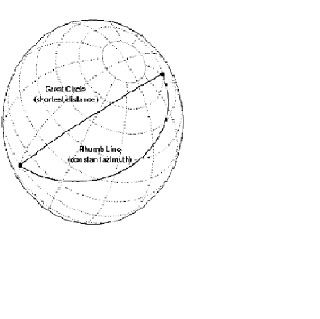
A great circle is the shortest path between two points along the surface of a sphere. The precise definition of a great circle is the intersection of the surface with a plane passing through the center of the planet. Thus, great circles always bisect the sphere. The equator and all meridians are great circles. All great circles other than these do not have a constant azimuth, they cross successive meridians at different angles. That great circles are the shortest path between points is not always apparent from maps, because very few map projections represent arbitrary great circles as straight lines.
A rhumb line is a curve that crosses each meridian at the same angle. Although a great circle is a shortest path, it is difficult to navigate because your bearing (or azimuth) continuously changes as you proceed. Following a rhumb line covers more distance than following a geodesic, but it is easier to navigate The following figure depicts a great circle and one possible rhumb line connecting two distant locations.
All parallels, including the equator, are rhumb lines, since they cross all meridians at 90º. Additionally, all meridians are rhumb lines, in addition to being great circles.
MAPS
A Mercator map can never fully show the polar areas, since linear scale becomes infinitely high at the poles. Being a conformal projection, the linear scale does not vary with direction and the angles are preserved around all locations. However, and like in any other map projection, scale varies from place to place, distorting the shapes of geographical objects. In particular, areas are strongly affected, transmitting a grossly distorted image of the geometry of our planet. All lines of constant bearing (rhumb lines or loxodromes), i. e., those making constant angles with the meridians, are represented by straight segments on a Mercator map. This is precisely the type of route usually employed by ships at sea, where compasses are used to indicate geographical directions and steer the ships. The two properties, conformality and straight rhumb lines, makes this projection uniquely suited to marine navigation: courses and bearings are measured using wind-roses or protractors, and the corresponding directions are easily transferred from point to point, on the map, with the help of a parallel ruler or a pair of navigational squares.

THE SUN AND THE EARTH
The Sun moves about 1° east per day on the celestial sphere. Over a year the Sun completes a great circle on the celestial sphere. The path of the Sun on the celestial sphere is called the ecliptic. The ecliptic is inclined about 23.5° compared to the celestial equator.
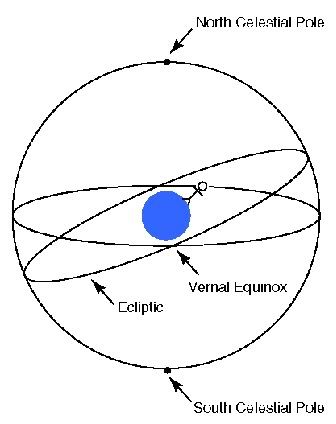
Thus during half the year the Sun is north of the celestial equator, and the Sun's daily path in the sky is like the red star on the below figure. During the other half of the year the Sun's daily path is like the green star.
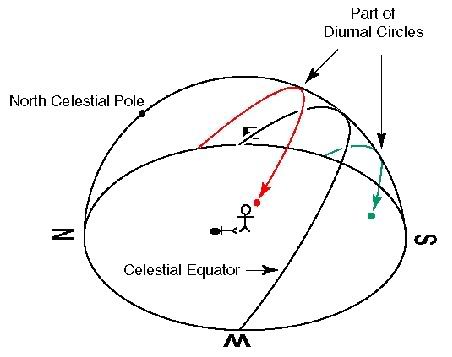
The moments, two each year, when the Sun moves between hemispheres are called equinoxes; one happens around March 21, the other around September 21. The spring equinox (when the Sun moves from the southern hemisphere to the northern hemisphere) is called the vernal equinox
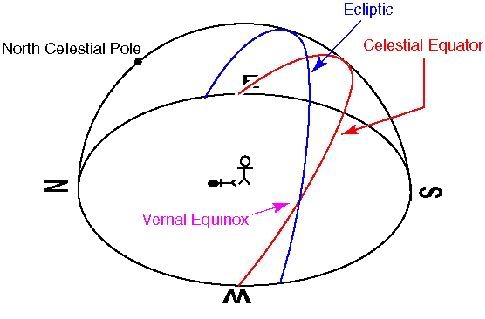
The Earth's spin axis is tilted by 23.5° with respect to the Earth's orbital plane (the ecliptic plane). The direction of Earth's spin axis is fixed in space.
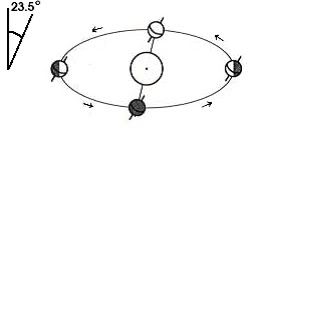
The tilt of the Earth's spin axis with respect to the ecliptic plane results in the Sun tracking out a sinusoidal path on the celestial sphere on the course of the year.
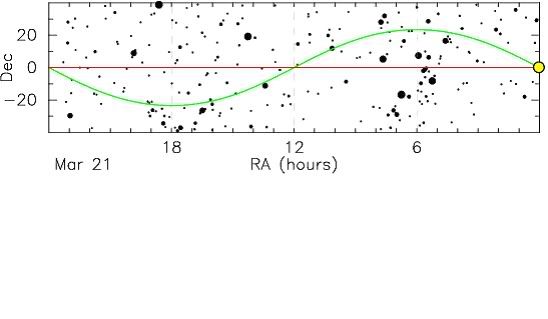
The word solstice means "Sun standing still"
The Sun traces its rising and setting positions north and south along the horizon in an annual pattern that is exactly repeatable and that recurs seasonally. Thus it provides a reliable and convenient calendar, like a pendulum oscillating around the points due east or due west. The risings, settings, and 12-hour durations cannot be exact, since the Sun is continuously moving along the ecliptic and is on the equinoxes but for the moment. In addition, upward refraction by the Earth's atmosphere and the finite angular diameter of the Sun renders the equinox day a bit longer than 12 hours, night a bit shorter, all the while ignoring twilight
Sunrises and sunsets reach their extreme northerly and southerly positions on the solstices; and occur due east and due west on the equinoxes.As the Sun moves south, it rises and sets progressively farther south of east and west. Northern hemisphere days now get shorter (less than 12 hours), nights longer (greater than 12 hours). On December 22, the Sun reaches its most southerly extent, at a declination of 23.4 degrees south, at the Winter Solstice to begin northern-hemisphere winter (southern hemisphere summer). It then rises as far south of east and sets as far south of west as possible. Northern- hemisphere daytime is now minimized, nighttime maximized. All the effects are reversed in the southern hemisphere, while at the Earth's equator, days and nights are always equal at 12 hours.
Summer. The Sun reaches maximum Southern Declination in the sky - exactly 23½° South Declination. It is this which defines the Tropic of Capricorn, a third belt which circles the Earth exactly 23½° below the Equator. The Antarctic circle and latitudes below are bathed in 24 hours of daylight, while the Arctic Circle and points above are having 24 hours of night.
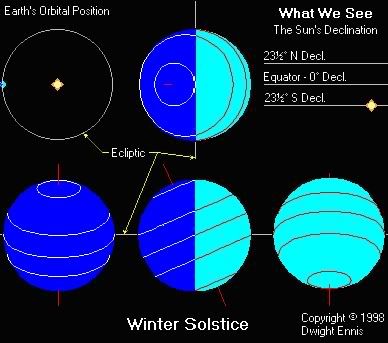
the reason for the varying length of the day throughout the year. This can be most clearly illustrated with another illustration.
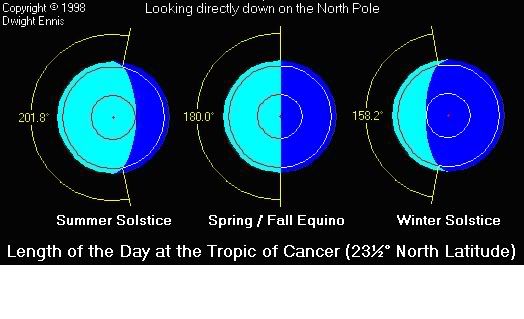
For simplicity, the above picture assumes one is located exactly on the Tropic of Cancer at 23½° north latitude. As can be seen, the angle of the Earth's surface contained within the daylight side varies with the time of year from 201.8° at the Summer Solstice to 158.2° at the Winter Solstice. Since the Earth rotates one full revolution, or 360° every 24 hours, we can calculate that it rotates 360/24=15° each hour. So, at the Summer Solstice, the longest day of the year, we have 201.8° of daylight, or 201.8°/15° per hour = 13.45 hours = 13 hours 27 minutes of daylight.
At the Winter Solstice, the shortest day of the year, the angle of daylight is only 158.2°. In this case, we have 158.2°/15° per hour = 10.55 hours = 10 hours 33 minutes of daylight.
Horizon: Wherever one is located on or near the Earth's surface, the Earth is perceived as essentially flat and, therefore, as a plane. The sky resembles one-half of a sphere or dome centered at the observer. If there are no visual obstructions, the apparent intersection of the sky with the Earth's (plane) surface is the horizon, which appears as a circle centered at the observer. For rise/set computations, the observer's eye is considered to be on the surface of the Earth, so that the horizon is geometrically exactly 90 degrees from the local vertical direction.
Sunrise and sunset conventionally refer to the times when the upper edge of the disk of the Sun is on the horizon, considered unobstructed relative to the location of interest. Atmospheric conditions are assumed to be average, and the location is in a level region on the Earth's surface.
Civil twilight is defined to begin in the morning, and to end in the evening when the center of the Sun is geometrically 6 degrees below the horizon.
PUTTING IT ALL TOGETHER
Calculations below are done using the suns position as 96 degrees west of Auckland ie 90 deg + 6 deg for civil twilight. And all are worked for Auckland because that is where the original screenshot post depicted and that's where I am and where all my info is.
This first map shows the great circle route between NZAA and the position over which the Sun is at ECT on the Summer Solstice ( approx Dec 22nd) and runs over southern Tasmania. Track = 247.5deg True = 227.4 deg Magnetic.
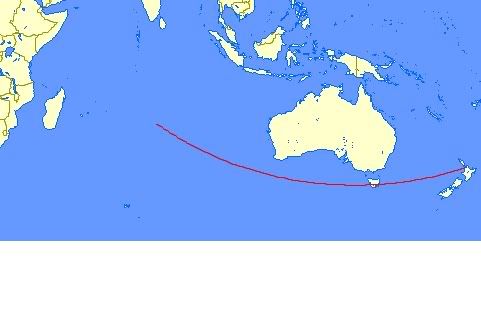
From To Distance
NZAA (37°00'29"S 174°47'30"E) 23°30'00"S 78°47'30"E 4847 nm
This 2nd map is worked out for last night (8th Jan 2007) as you can see the course now runs further north across the top of Tasmania .This is because approx 16 days have passed so the suns path is 16/91x23.5 further north ie 4.23 degrees so it is now about 19.27degrees S
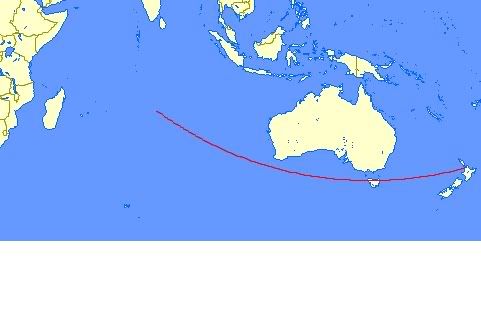
From To Distance
NZAA (37°00'29"S 174°47'30"E) 19°24'00"S 78°47'30"E 4994 nm
As we progress into winter the Sun sets further and further north until it reaches the Winter Solstice position (23.5 degrees N) and is nearly along the NZAA "“ Brisbane track. ( even the bloody sun heads for the gold coast in winter!)
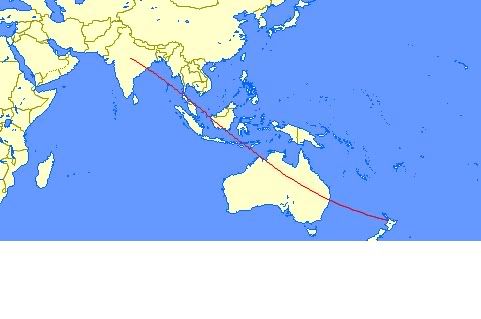
From To Distance
NZAA (37°00'29"S 174°47'30"E) 23°30'00"N 78°47'30"E 6509 nm
Well that about wraps it up, I hope that this has cleared up a few points for people and maybe given a few of you the start of an interest in navigation and all its intricacies. If anyone has questions then the forums are always there and I am sure there are other guys (and girls) out there with a heap more detailed knowledge than I have that are willing to help if asked.
Cheers all
